개체의 식별
메타데이터 이용해서 속성의 동일성 여부를 판단한다.
하나의 데이터를 두 개로 쪼갤 때 보는 게 함수적 종속 관계
-명제 이야기
–
x = {x1, x2} y = {y1, y2}
x1 = x2 –> y1 = y2를 보장한다면 (어떤 상황에도 True)
x –> y 이다. x를 결정자, y를 의존자라고 한다.
-고객 번호는 고객 명을 결정한다. 111 –> 홍길동
-반면에 고객명 –> 고객번호 ?
반례를 찾으면 된다.
동명이인의 경우에는 성립되지 않는다.
-대우는 성립하지만 역은 항상 성립하지 않는다.
![]()
중복
상관계수: -1 ~ 1 사이
1에 가까울수록 양의 상관도를 갖는다는 뜻
뚜렷한 비례 혹은 반비례 관계를 갖는다.
A,B 상관관계 높다면 A만 분석하면 B를 경향성을 통해 예측할 수 있다.
어떻게든 분석하기 위한 속성을 줄이기 위한 노력
범주형 데이터
A, B 속성
관측도수: 실제 존재하는 튜플 수
기대도수: 확률적으로 기대되는 튜플 수
두 속성에 상관관계가 있다. (대립가설)
없다 : 귀무가설
자유도: 속성등의 cardinality
cardinality: the number of distinct value
A의 cardinality: the number of distinct values in A
cardi(A) = a, card(B) = b라 하면 자유도 = (a-1)(b-1)
자유도에 따라 기준되는 통계량이 다르다.
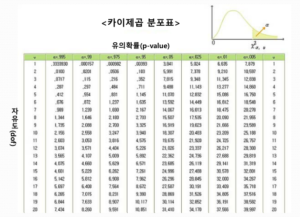
a = 0.05이고 자유도가 1이라면 카이제곱값이 3.841을 넘을 때 상관관계가 있다고 판단한다.
카이제곱 예제에서 자유도는 (2-1) * (2-1) = 1
여기에서 0.05에 해당하는 유의확률은 3.841
그런데 값은 507.93 겁나 큼. 누가 봐도 연관성 강함.